Опубликована в журнале "Измерительная техника" – 2006. -№ 1
О.Л. Рутенберг, Ш.Р. Фаткудинова, С.В. Вихрова,
Всероссийский научно-исследовательский институт метрологической службы, ул. Озёрная, д.46, г. Москва, 119361, РФ
e-mail:analyt-vm@vniims.ru
В.С. Морозов, Е.В. Морозов
ЗАО «Научно-техническое агентство «Наука», ул. Сельскохозяйственная, 12, г. Москва, 129226, РФ
e-mail: nauca@nauca.ru
Гигрометрия в единицах термометрической шкалы
Обоснованo использование для количественной характеристики влажности газа, выраженной в единицах термометрической шкалы, только одного термина – "точка росы". Охарактеризованы особенности и условия корректного применения этого термина, а также расчетные методы оценки параметров фазового равновесия в системе вода в конденсированном состоянии – сжатый газ.
Ключевые слова: гигрометрия, влажность газа, точка росы, фазовое равновесие.
The application only the term "dew point" for quantitative characteristic of gas moisture is founded. The features and the conditions of the correct application of the term as well as the calculation methods of the estimation of phase equilibrium parameters in the system condensed water – compressed gas are described.
Key words: hygrometry, gas moisture, dew point, phase equilibrium.
В отечественной технической литературе и нормативных документах встречаются разнообразные названия характеристики влажности газа, выраженной в единицах термометрической шкалы: точка росы [1–4], температура насыщения [5], точка льда (инея) [4] и т. п. Поскольку всегда речь идет фактически об одной и той же характеристике влажности газа, целесообразно остановиться на одном термине – "точка росы", что в полной мере соответствует запросам практической гигрометрии (с учетом присущих этому термину особенностей).
Особенности применения термина "точка росы"
Термин "точка росы" в качестве характеристики влажности газа, выраженной в единицах термометрической шкалы, введен в гигрометрию в связи с созданием конденсационного гигрометра, предназначенного изначально для анализа атмосферного воздуха. В определении точки росы, приведенном в [1, 2], фигурирует только влажный воздух, примеры в [2] охватывают только положительные температуры по шкале Цельсия. В действовавшем до недавнего времени стандарте [3] дано следующее определение точки росы: "Точка росы – температура, при которой водяной пар во влажном газе, охлаждаемом изобарически, становится насыщенным". В соответствии с [4] точку росы обозначают $t_{d}$.
Из такого определения следует, что представлению $t_{d}$ в численном виде должен предшествовать перевод данной макроскопической гомогенной двухкомпонентной системы газ – водяной пар из начального состояния в конечное состояние насыщения путем изобарического охлаждения. При этом речь идет о температуре конечного равновесного состояния системы, а не о температуре, при которой фазовый переход в ней фактически начинается.
Система в конечном равновесном состоянии представляет собой газовую фазу, соприкасающуюся с плоской поверхностью влаги в конденсированном состоянии, имеющую одинаковые с рассматриваемой системой значения температуры и давления. Последствием такого соприкосновения будет только изменение характера равновесия. Из статического равновесия система перейдет в состояние двухфазного динамического равновесия. Система в таком состоянии в соответствии с правилом фаз Гиббса [6] является дивариантной, т. е. имеет две степени свободы. Отсюда следует, что численному значению $t_{d}$ при данной влажности газа обязательно должны сопутствовать еще и сведения о давлении газа.
Более того, одному и тому же значению $t_{d}$ при данном давлении могут соответствовать неодинаковые значения содержания влаги в различных по своей природе газах. В табл. 1 представлены взятые из [7] экспериментальные данные о равновесных значениях объемной доли влаги в таких газах, как Н₂, N₂, CH₄ и СО₂ при $t_{d}$ = 50°С и давлениях 10 и 50 МПа.
Таблица 1
Экспериментальные данные о равновесных значениях влаги в газах
Давление, МПа | Объемная доля влаги, млн⁻¹ | |||
Н₂ | N₂ | CH₄ | СО₂ | |
10 | 1380 | 1560 | 1900 | 3200 |
50 | 400 | 620 | 740 | 6550 |
Из табл. 1 видно, что при одном и том же значении $t_{d}$ объемная доля влаги зависит от природы и давления газа и, следовательно, приводить только значение точки росы без указания давления и природы газа некорректно, поскольку невозможно однозначно интерпретировать полученные данные.
Одним из способов решения этой проблемы является приведение значения $t_{d}$, соответствующее реальному давлению газа, к значению $t_{d\,101,3}$, соответствующему нормальному давлению 101,3 кПа. При нормальном давлении поведение многих технических газов и их смесей мало отличается от поведения идеального газа. В таком случае отпадает необходимость в указании природы газа, а полученное значение $t_{d\,101,3}$ достаточно просто переводить в соответствующие значения других характеристик влажности (объемных долей, влагосодержания, абсолютной влажности и т. д.). Соответственно, упрощается сравнительная оценка гигрометров различного принципа действия и обеспечивается возможность однозначной интерпретации результатов измерений влажности газов.
Приведение значений $t_{d}$ к $t_{d\,101,3}$ может быть выполнено с использованием как математических зависимостей значений $t_{d}$ от параметров состояния по кривым фазовых равновесий, так и соответствующих табличных, расчетных или экспериментальных данных, номограмм и т.п.
Примером представления влажности газов в виде $t_{d\,101,3}$ могут служить гигрометры ИВА-8 и ИВА-9, в которых необходимые расчеты выполняются автоматически.
Возможности расчетных оценок характеристик влажности газов
Расчеты, указанные выше в качестве необходимых, являются предметом теории и практики фазовых равновесий. К сожалению, состояние теории здесь такое, что в широкой области параметров предсказание возможно с получением только качественных результатов. Действительно, "фазовое равновесие в смесях газов и жидкостей – предмет непростой" ([8], стр. 343). Количественные результаты расчетов можно получить либо с привлечением экспериментальных данных, либо с использованием адекватных физических моделей системы. Ниже рассмотрена упрощенная модель двухкомпонентной двухфазной системы, применение которой приводит в ряде случаев к практически важным результатам.
Пусть данный газ (компонент 1) не вступает в химическое взаимодействие с водой (компонент 2). В конденсированном состоянии вода не растворяет заметно газ, т. е. является веществом чистым. Ее мольный объем в конденсированном состоянии $V_{2\,конд}^{0}$ не зависит от давления ${р}$ в системе, т. е. в таком состоянии вода является несжимаемой. Чистый насыщенный пар воды под давлением ${p}_{2\,нас}^{0}$ является идеальным газом, а значение ${p}_{2\,нас}^{0}\ll{p}_{}$. Вода в конденсированном состоянии находится в термодинамическом равновесии с ее газовым раствором. Переохлажденное квазиравновесное состояние воды здесь не рассматривается.
Тогда применение общих термодинамических выражений в соответствии с [7] приводит к следующему уравнению:
где $F$ – фактор увеличения произведения ${p}x_{2}$ по отношению к $p_{2 нас}^{0}$ ($px_{2}$ равно парциальному давлению паров воды в газовой смеси);
$V, V_{ид}$ – мольные объемы газовой смеси при давлении $p_{}$ и температуре $T\left(T=273,15+t_{d}°C\right)$ и в идеальном состоянии, соответственно;
$x_{1},\,x_{2}$ – мольные (объемные) доли газа и влаги в газовой смеси, соответственно;
$R$ – газовая постоянная;
индекс «0» относится к чистому веществу.
Уравнение (1) в границах принятых при его выводе условий позволяет выполнять расчеты всех необходимых характеристик влажности газов, если известны значения $P_{2\,нас}^{0}$ и ${p}-{V}-{T}-{x}$ – данные для исследуемой системы. Такие данные можно получить экспериментально или рассчитать с помощью подходящей теоретической модели.
Ниже рассмотрены некоторые теоретические модели, которые в сочетании с (1) могут быть использованы для практических расчетов.
Модель 1
$V_{2\,конд}^{0}=0$; газовая фаза – идеальный газ.
Тогда из (1) следует, что
Уравнения (2) соответствуют открытому еще в 1801 г. закону Дж. Дальтона.
Модель 2
$V_{2\,конд}^{0}\neq 0$; газовая фаза – идеальный газ.
В таком случае из (1) получим
Экспоненциальный множитель в (3) называется поправкой Пойнтинга.
Модель 3
$V_{2\,конд}^{0}\neq 0$; газовая фаза является бесконечно разбавленным раствором, т. е.
и подчиняется уравнению состояния со вторым вириальным коэффициентом
где $B$ – второй вириальный коэффициент, зависящий только от температуры и состава газовой смеси. Для двухкомпонентной смеси
где $B_{11},\,B_{22}$ – вириальные коэффициенты чистых компонентов 1 и 2;
$B_{12}$ – вириальный коэффициент, характеризующий взаимодействие молекул 1 и 2.
В данном случае решением уравнения (1) будет выражение
На основе приведенных выше моделей, а также экспериментальных данных [9] рассчитали значения $t_{d}$ для азота с объемной долей влаги 1,0 млн⁻¹ в области давлений (0,05–20) МПа. В расчетах использовали известную зависимость $p_{2\,нас}^{0}$ от температуры [4], значение $V_{2\,конд}^{0}=19,5$ см³/моль [10] и вычисленные в соответствии с [11] значения $B_{11}$ и $B_{12}$. Зависимость от давления отклонений Δ$t_{d}$ значений $t_{d}$, расcчитанных в соответствии с описанными выше моделями, от вычисленных по данным [9], приведена на рисунке.
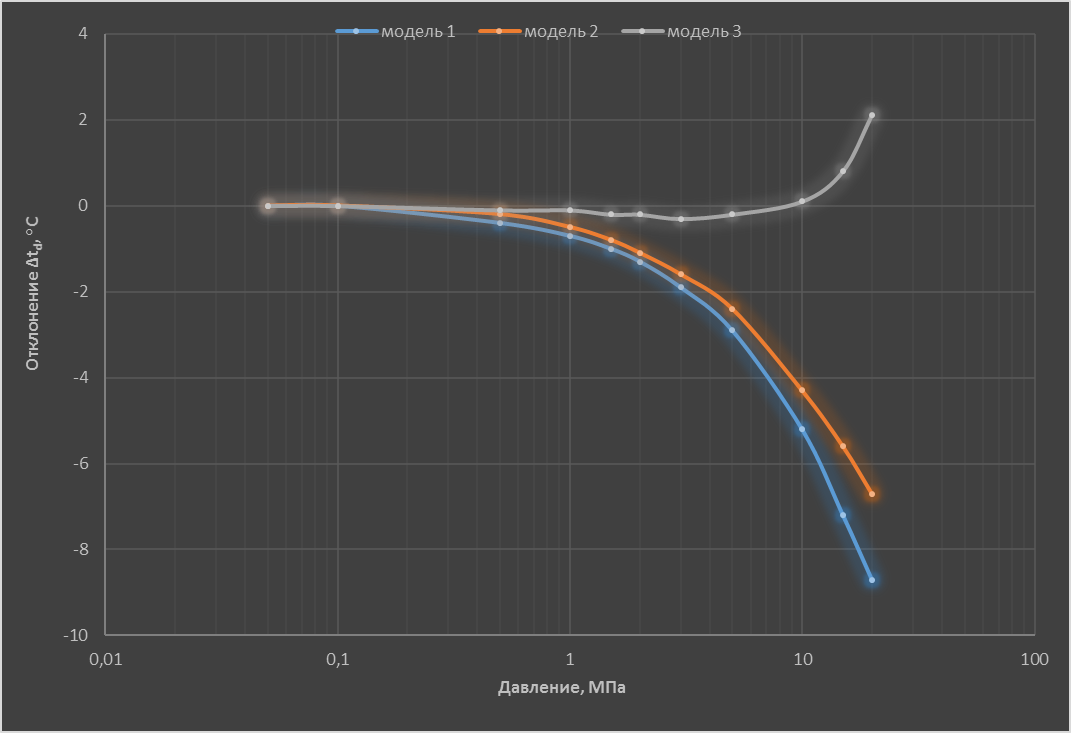
Рисунок. Зависимость расчетных значений Δ$t_{d}$ от давления при объёмной доле влаги в азоте $x_{2}$=1 млн⁻¹.
Показано, что для азота существует область относительно невысоких давлений, для которых использование рассмотренных моделей дает результаты, совпадающие в пределах погрешности с данными [9]. По оценке авторов, в области объемной доли влаги до 100 млн⁻¹ такое поведение справедливо для воздуха, кислорода, гелия, неона, водорода. Причем для гелия, неона и водорода расчеты по моделям 1 и 2 дают согласованные результаты при более высоких давлениях, чем для азота.
Применение указанных моделей без учета предварительно установленных ограничений в области давлений может привести к ошибочным результатам. Например, содержание влаги в сжатом до 15,0 МПа азоте $t_{d}$ = –65°С измерили конденсационным гигрометром. Далее рассчитали соответствующие значения объемной доли влаги $x_{2}$ и значения $t_{d\,101,3}$. Результаты расчета, приведенные в табл. 2, показывают, что наименьшее отклонение от данных [9] у результатов вычислений с использованием модели 3. Применение моделей 1 и 2 дает близкие отклонения от данных [9], составляющие для $t_{d\,101,3}$ приблизительно –4,5°С, а для $x_{2}$ - 60%, а для $t_{d\,101,3}$ - приблизительно (-4,5)°С.
Таблица 2
Результаты расчетов $x_{2}$ и $t_{d\,101,3}$ для азота, содержание влаги в котором соответствует $t_{d}$ = –65°С
Характеристика влажного газа | Расчетное значение содержания влаги в азоте | |||
модель 1 | модель 2 | модель 3 | данные [9] | |
$x_{2}$, млн⁻¹ | 3,60·10⁻² | 4,26·10⁻² | 11,0·10⁻² | 9,46·10⁻² |
$t_{d\,101,3}$, °C | –95,2 | –94,3 | –89,4 | –90,1 |
Таким образом, имеется достаточно оснований в практической гигрометрии использовать один термин "точка росы" в качестве количественной характеристики влажности газа, выраженной в единицах термометрической шкалы. Этот термин имеет длительную историю применения, корректное в термодинамическом отношении определение и обозначается как $t_{d}$. Численному значению $t_{d}$ должны сопутствовать сведения о давлении газа и его природе, отсутствие которых ведет к неоднозначному толкованию полученных результатов.
Целесообразно значение $t_{d}$ приводить путем расчетов к значению $t_{d\,101,3}$. Такой прием находит практическое применение, но требует наличия надежных методов расчета. Основу таких расчетов могут составить как данные экспериментальных исследований фазовых равновесий в системах газ – вода, так и различные теоретические физические модели, адекватно представляющие свойства таких систем.
Результаты выполненных расчетов показывают, что для ряда технических газов существует область физических параметров, в которой может быть оправданным использование относительно простых известных моделей.
Литература
1. Толковый словарь по химии и химической технологии. Основные термины / Под ред. Ю. А. Лебедева. – М.: Русский язык, 1987.
2. Физический энциклопедический словарь. – М.: Сов. энциклопедия, 1983.
3. ГОСТ 8.221 – 76. ГСИ. Влагометрия и гигрометрия. Термины и определения.
4. ГОСТ 8.524 – 85. ГСИ. Таблицы психрометрические. Построение, содержание, расчетные соотношения.
5. ГОСТ 9293 – 74. Азот газообразный и жидкий. Технические условия. Изм. 1,2,3.
6. Герасимов Я.И. и др. Курс физической химии. Т. 1. – М.: Госхимиздат, 1963.
7. Кричевский И.Р. Фазовые равновесия в растворах при высоких давлениях. – М., Л.: Госхимиздат, 1946.
8. Рид Р., Праусниц Дж., Шервуд Т. Свойства газов и жидкостей. – Л.: Химия, 1982.
9. Иомтев М.Б. и др. Таблицы рекомендуемых справочных данных. Системы газ – лед. Растворимость льда в азоте и воздухе в диапазонах температур от –50 до – 2 °С и давлении от 0,2 до 61 МПа. ГСССД № Р88–84. – М: Изд-во стандартов, 1984.
10. Hyland R. W. // J. Rec. NBS. – 1975. – 79A. – № 4. – P. 551.
11. Гиршфельдер Дж., Кертис И., Берд Р. Молекулярная теория газов и жидкостей. – М.: ИИЛ, 1961.
Цены на водород ОСЧ по ТУ 2114-016-78538315-2008 «Водород особо чистый»
- Марка А (99,99999 %об.)1750 ₽ за м³
- Марка Б (99,9999 %об.)1460 ₽ за м³
- Марка В (99,999 %об.)1110 ₽ за м³
- Подготовка баллона к заполнению водородом марки А5016 ₽
- Подготовка баллона к заполнению водородом марки Б4218 ₽
- Подготовка баллона к заполнению водородом марки В2679 ₽
- Цены приведены с учетом всех налогов и сборов
