В.С. Морозов, Е.В. Морозов
ООО «Научно-производственная компания «Наука»
e-mail: nauca@nauca.ru
Особенности гигрометрии в единицах термометрической шкалы
Только численное значение точки росы, пусть и с размерностью в градусах термометрической шкалы, не несет определенной информации о влажности газа.
Ключевые слова: гигрометрия, влажность газа, точка росы, фазовое равновесие.
1. ВВЕДЕНИЕ
Успехи в области новых высоких технологий в значительной степени обусловлены применением технических газов и их смесей, влажность которых составляет предельно низкие значения. Для характеристики влажности таких газов находят применение как молярная (объемная) доля влаги, так и точка росы.
Молярная (объемная) доля влаги в газе является физической величиной, значение которой характеризует состав однофазной системы вне зависимости от значений ее физических параметров или природы составляющих систему компонентов. Значение такой величины является исчерпывающим источником информации о влажности газов и применяется в науке и технике, как в безразмерном виде, так и с размерностью в %, млн⁻¹, блн⁻¹.
С точки зрения метрологии [1], в качестве меры величины влажности газов в виде молярной (объемной) доли влаги могут быть эталонные или стандартные образцы состава, а также поверочные газовые смеси (ПГС). При практической реализации таких образцов или ПГС в области низких значений влажности учитывают высокие адсорбционные свойства влаги. Этим обусловлено использование в таком случае не статических, а динамических методов приготовления образцов или ПГС.
По сравнению с молярной (объемной) долей влаги, характеристика влажности газа в виде точки росы обладает целым рядом особенностей, которые следует учитывать как в гигрометрии, так и в инженерной практике. Представляется по этому важным обсудить эти особенности, исходя из имеющихся определений термина точка росы.
2. ОПРЕДЕЛЕНИЕ ТОЧКИ РОСЫ
Наиболее полным и термодинамически корректным, на наш взгляд, является определение точки росы в соответствии с [2], где "точка росы — температура, при которой водяной пар во влажном газе, охлаждаемом изобарически, становится насыщенным". При этом "насыщенный водяной пар во влажном газе" в [2] представлен как "водяной пар во влажном газе, находящийся в состоянии равновесия с плоской поверхностью воды".
В [3] содержится близкое по смыслу к [2] определение точки росы, правда без упоминаний о требовании постоянства давления газа при его охлаждении и геометрии поверхности воды, зато учитывается агрегатное состояние воды в виде жидкости или льда.
3. ОСОБЕННОСТИ ХАРАКТЕРИСТИКИ ВЛАЖНОСТИ В ВИДЕ ТОЧКИ РОСЫ
Наличие требования постоянства давления (без ограничений его величины) в представленном выше определении точки росы обусловлено тем, что значение температуры насыщенного состояния влажного газа зависит от абсолютного давления. Тогда, при одном и том же влагосодержании газа и прочих одинаковых условиях для каждого значения давления газа будет свое значение температуры насыщения, тем самым своё значение точки росы.
На рис. 1, для примера, представлена расчетная зависимость температуры насыщения (точки росы) от давления идеального газа, объёмная доля влаги в котором составляет 0,1 млн⁻¹. Видим, что при изменении давления от 0,1 МПа до 10 МПа значение точки росы изменяется, соответственно, от -90°С, до -60,5°С при одной и той же влажности газа.
Таким образом, только численное значение точки росы, пусть и с размерностью в градусах термометрической шкалы, не несет определенной информации о влажности газа.
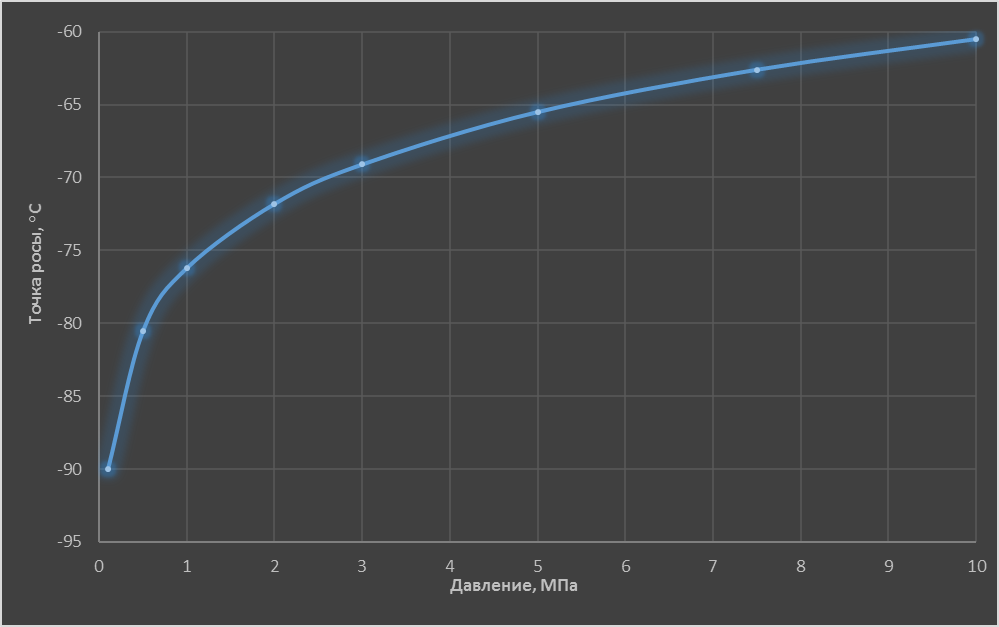
Рис. 1.
На рис. 2 представлены данные о зависимости равновесных со льдом значений молярной доли влаги от давления при одной и той же температуре -50°С, как для идеального газа (расчет), так и для воздуха (в соответствии с экспериментальными данными работы [4]).
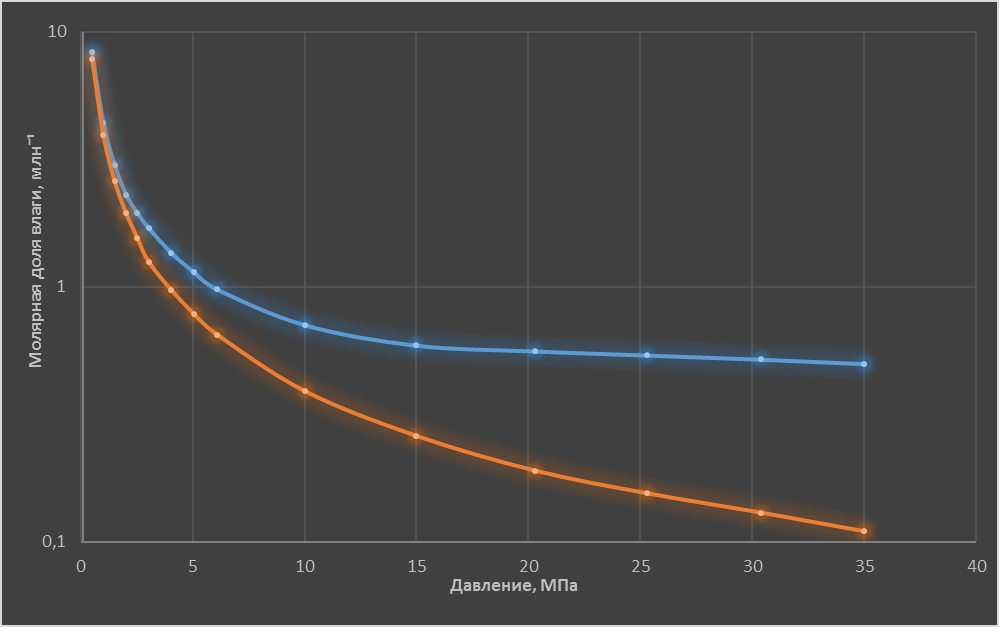
Рис. 2.
Здесь наблюдаем, что увеличение давления приводит к увеличению отличий значений растворимости льда в идеальном газе и в реальном воздухе. Так, при давлении 10 МПа растворимость льда в воздухе в 1,9 раза выше, чем в идеальном газе, а при давлении 35 МПа - в 4,5 раза (!).
Таким образом, в общем случае, даже при наличии сведений о величине давления, значение точки росы не является определенной характеристикой влажности газа, если нет сведений о каком, собственно, газе идет речь. Однако, и это еще не всё. Поскольку в определении точки росы речь идет о предполагаемом мысленно наступлении состояния насыщения относительно плоской поверхности воды, значение точки росы, при прочих одинаковых условиях, зависит от представлений о чистоте конденсированной фазы, а также о её состоянии в термодинамическом отношении — стабильное (вода, лёд) или лобильное (переохлажденная вода).
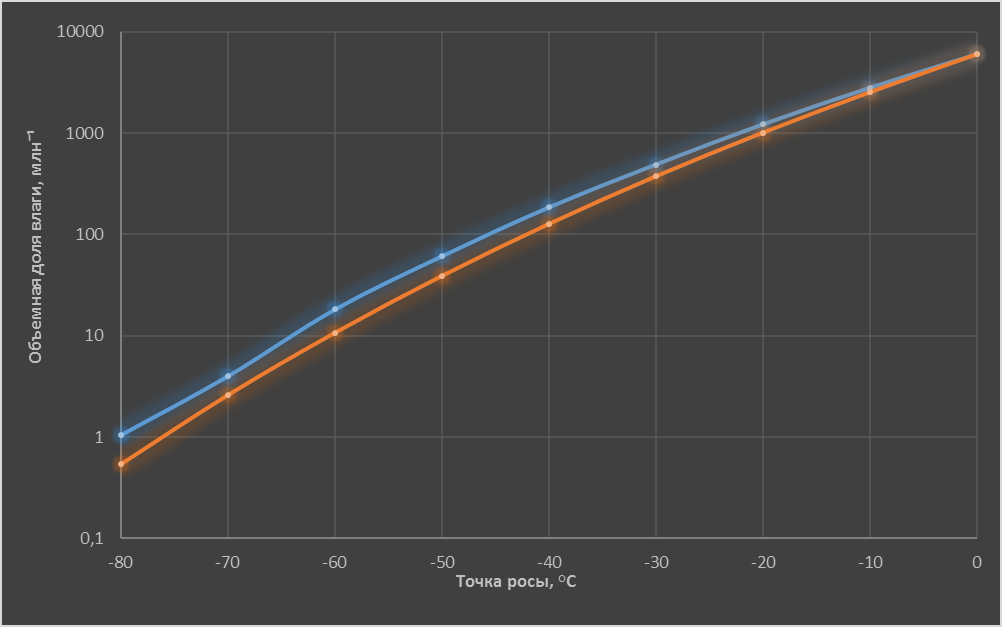
Рис. 3.
На рис. 3 представлены результаты расчета объёмной доли влаги в идеальном газе при нормальном давлении 101,3 кПа в зависимости от значений точки росы для чистой переохлажденной воды и для одинаково чистого льда, имеющих плоскую поверхность.
Видим, что при одних и тех же прочих условиях влажность газа относительно переохлажденной воды выше, чем относительно льда. При значении точки росы -80°С отличие составляет приблизительно в 2 раза.
На конкретных примерах можно также показать, какое влияние на значение точки росы оказывают представления о чистоте конденсированной фазы и геометрии её поверхности. Здесь, однако, остановимся на примере, иллюстрирующем к каким последствиям может привести мысленный (виртуальный) характер выражения влажности газа в виде точки росы. Пусть рассматриваемым газом будет двуокись углерода, объёмная доля влаги в котором составляет 0,5 млн⁻¹. Если исходить из модели идеального газа и представлений о насыщенном состоянии водяного пара относительно плоской поверхности чистого льда, расчетная величина точки росы при нормальном давлении 101,3 кПа составит -80,5°С. Однако, температура сублимации двуокиси углерода при указанном давлении составляет -78,45°С, т.е. при температуре -80,5°С и давлении 101,3 кПа реально возможным состоянием двуокиси углерода является твердое состояние, а никак не газообразное. Соответственно, обречены на неудачу в рассматриваемом случае попытки для определения влажности применить конденсационный гигрометр, поскольку в согласии с данными о сублимации двуокиси углерода реально охлаждаемая в конденсационном гигрометре поверхность (зеркало) покроется твердой двуокисью углерода раньше, чем сможет конденсироваться влага. С другой стороны, газообразная двуокись углерода с весьма малой влажностью является востребованной в науке и технике. При этом реализуется и аналитический контроль её влажности, правда, гигрометрами иного, чем конденсационный, принципа действия, в том числе со шкалой в единицах точки росы. Последнее является иллюстрацией того, что гигрометрия в единицах термометрической шкалы имеет практический смысл даже в таком явно казусном случае, как в примере с двуокисью углерода. Придать такой смысл характеристике влажности газа можно, если в той или иной мере учесть обозначенные выше особенности понятия точки росы.
4. ПРИДАНИЕ ПРАКТИЧЕСКОГО СМЫСЛА ВЕЛИЧИНЕ ТОЧКИ РОСЫ
Для качественной оценки степени влажности данного газа по величине точки росы необходимым и достаточным является соблюдение условия, чтобы при различных значениях точки росы давление было одинаковым. Только тогда, чем выше значение точки росы, тем более влажным является такой газ.
Для решения обозначенной качественной задачи является также вполне достаточным, если значения точки росы при разных давлениях приводить к её значению при одном выбранном в качестве постоянного давлении, например, к значению при нормальном давлении 101,3 кПа. Реализация такой процедуры, а также решение количественной задачи (определения влажности по какому-либо значению точки росы при данном давлении) осуществимы, если значение точки росы отождествить с температурой двухфазного равновесия с участием конденсированной фазы воды (льда). Иными словами, мысленно привести в соприкосновение данный газ с водой (льдом) при данном давлении и температуре, равной значению точки росы. При таком подходе открываются два пути.
Один из них заключается в том, что в таком случае можно прямо использовать имеющиеся в литературе экспериментальные данные о растворимости воды (льда) в газах. К сожалению, из-за экспериментальных трудностей набор таких данных весьма ограничен.
Второй путь — использовать расчетный метод, основу которого составляет адекватная физическая модель двухфазной системы.
В области низких влагосодержаний к практически приемлемым результатам расчетов приводит гипотеза о конденсированной фазе, как о веществе твёрдом (лёд), чистом, несжимаемом, химически не взаимодействующем с газом и имеющем плоскую поверхность раздела с равновесно сосуществующей газовой фазой, поведение которой описывается одним из известных уравнений состояния. Такая гипотеза позволяет термодинамическим методом выявить зависимость влажности газа от параметров состояния.
Действительно, с точки зрения термодинамики [5], условием химического равновесия двух фаз является равенство химических потенциалов каждого компонента в обеих фазах. Если стандартные состояния компонента в обеих фазах приняты одними и теми же, то равенство химических потенциалов эквивалентно равенству летучестей этого компонента в обеих фазах. Применительно к нашему случаю условие химического (фазового) равновесия для чистого твердого вещества 2 (лёд) в растворителе 1 (газ) запишется в виде:
где $f_{2}$ и $f_{2,\,тв}^{0}$ – летучести вещества 2, соответственно, в газовой и в чистой твердой фазах.
Рассмотрим каждую из частей равенства (1) в отдельности.
При постоянной температуре $T_{}$ зависимость $f_{2,\,тв}^{0}$ от давления $P_{}$ можно выразить следующим термодинамическим уравнением:
где $V_{2,\,тв}^{0}$ — молярный объём чистого твердого вещества 2, $R_{}$ — газовая постоянная.
Для вычисления $f_{2,\,тв}^{0}$ при давлении, отличном от давления насыщенного пара $P_{2,\,нас}^{0}$, проинтегрируем (2) в пределах от $P_{2,\,нас}^{0}$ до $P_{}$. Учитывая условие несжимаемости льда, получим:
Летучесть $f_{2,\,тв}^{0}\left ( P_{2,\,нас}^{0} \right )$ чистого твердого вещества 2 при температуре $T_{}$ и давлении $P_{2,\,нас}^{0}$ равна летучести находящегося с ним в равновесии пара $f_{2}^{0}\left ( P_{2,\,нас}^{0} \right )$, т.е.
Для летучести чистого пара (газа) справедливо следующее термодинамическое уравнение:
$V_{ид}$ — объём идеального газа, вычисленный для того же давления, при котором берется $V_{2}^{0}$.
Если принять, что поведение чистого пара вещества 2 подчиняется законам идеального газа, то $V_{2}^{0}=V_{ид}$ и из (5) и (4) следует, что
Для случая, когда $P_{2,\,нм}^{0}\ll P$, подстановкой (6) в (3) получим:
Когда независимой переменной является давление $P_{}$, для нахождения летучести вещества 2 в газовом растворе при постоянной температуре $T_{}$ удобно воспользоваться следующим общим термодинамическим уравнением, записанным для двухкомпонентной системы в виде:
$V_{}$ - его молярный объём, а $V_{ид}$ - объём идеального газа, вычисленный для того же давления, при котором берется $V_{}$.
Подстановкой (7) и (8) в (1) получаем следующее итоговое уравнение:
Здесь абсолютная температура $T=273,15° + t_{d}°C$, где $t_{d}°C$ - значение точки росы в °С.
Уравнение (9) позволяет, с учетом принятых при его выводе условий, рассчитывать все необходимые характеристики влажности газов, в том числе определить $t_{d}$ при данных $P_{}$ и $X_{2}$, определить, $X_{2}$ при известных $t{d}$ и $P_{}$, а также выполнить переход от значения $t{d}$ при одном давлении (при одной и той же влажности $X_{2}$) к значению $t{d}$ при другом давлении.
Однако, для выполнения таких расчетов необходимо располагать сведениями о зависимости упругости паров льда от температуры $P_{2,\,нас}^{0}\left( T\right)$, его молярном объёме $V_{2,\,тв}^{0}$ и об уравнении состояния смеси водяного пара с данным газом.
Создатели и пользователи гигрометров со шкалой влажности в единицах точки росы, как правило, пренебрегают значением молярного объёма льда и применяют уравнение состояния идеального газа. В таком случае решением уравнения (9) является уравнение Дальтона (1801 г.)
В работе [6] показано, что для ряда технических газов существует область относительно невысоких давлений, когда расчеты в соответствии с (10) приводят к практически приемлемым результатам. Однако, чем выше давление в системе, тем больше результаты упрощённых расчетов могут отличаться от реальной картины (см. данные на рис. 2). Это побуждает применять более сложные физические модели рассматриваемой системы.
Таким образом, при реализации расчетного пути придания практической значимости выражению влажности газа в виде точки росы необходимо проявлять осторожность, особенно при высоких давлениях. Однако, для обеспечения возможности реализации того или иного пути, наряду с представлением значения точки росы, является обязательным представление данных о величине абсолютного давления газа.
Изложенное выше представляется необходимым учитывать и в метрологии при решении проблемного, на наш взгляд, вопроса создания самостоятельной меры величины влажности газов в виде точки росы.
ЛИТЕРАТУРА
1. РМГ 29-99. Метрология. Основные термины и определения.
2. ГОСТ 8.221-76 Влагометрия и гигрометрия. Термины и определения.
3. ISBN 0-904457-24-9 A guide to the measurement of humidity. The Institute of Measurement and Control, London, 1996.
4. Иомтев М.Б., Пискунов В.Г., Каджаев В.Л., Гордеев И.В., Губанова Г.П. Таблицы рекомендуемых справочных данных. Системы газ-лёд. Растворимость льда в азоте и воздухе в диапазонах температур от -50 до -2°С и давлений от 0,2 до 61 МПа. ГСССД № Р88-84.-М: Изд-во стандартов, 1984.
5. Кричевский И.Р. Фазовые равновесия в растворах при высоких давлениях. Госхимиздат. М.-Л., 1952, 168 стр.
6. Морозов В.С., Морозов Е.В., Рутенберг О.Л., Фаткудинова Ш.Р., Вихрова С.В. Гигрометрия в единицах термометрической шкалы. Измерительная техника, № 1, 2006, 46-48.
Цены на водород ОСЧ по ТУ 2114-016-78538315-2008 «Водород особо чистый»
- Марка А (99,99999 %об.)1750 ₽ за м³
- Марка Б (99,9999 %об.)1460 ₽ за м³
- Марка В (99,999 %об.)1110 ₽ за м³
- Подготовка баллона к заполнению водородом марки А5016 ₽
- Подготовка баллона к заполнению водородом марки Б4218 ₽
- Подготовка баллона к заполнению водородом марки В2679 ₽
- Цены приведены с учетом всех налогов и сборов
